COLLOQUIO ESAMI DI STATO
DOMANDE CON RELATIVE RISPOSTE DI
ANALISI
MATEMATICA (STUDIO DI UNA FUNZIONE)
DOMANDA N.1: Quali sono le funzioni fratte per le quali il Dominio si
trova imponendo al loro Denominatore d’essere diverso da zero ?
RISPOSTA: Risultano essere le funzioni algebriche razionali fratte, le
funzioni algebriche irrazionali(con indice dispari) fratte, le funzioni
trascendenti goniometriche fratte(non irrazionali ad indice pari) e le funzioni
trascendenti esponenziali fratte(non irrazionali ad indice pari).
DOMANDA N.2: Quali sono le
funzioni per le quali il Dominio si
trova risolvendo una Disequazione ?
RISPOSTA: Risultano essere le
funzioni algebriche irrazionali ad indice pari e le funzioni trascendenti
logaritmiche
DOMANDA N.3: In quali passi dello Studio di una Funzione si utilizza
una disequazione ?
RISPOSTA:
a)
Nella ricerca del
Dominio per le funzioni(vedi Domanda n.2) algebriche irrazionali ad indice pari
e le funzioni trascendenti logaritmiche;
b)
Per cercare il
segno di una funzione y=f(x) e precisamente s’impone y>0 per trovare gli
intervalli ove la funzione è positiva. La risoluzione di tale disequazione restituisce anche gli intervalli dove la
funzione è negativa (y<0);
c)
Per cercare gli
intervalli dove la funzione è crescente (imponendo alla derivata prima d’essere
positiva ovvero y’>0). La
risoluzione di tale disequazione restituisce anche gli intervalli dove la
funzione è decrescente (y’<0);
d)
Per cercare gli
intervalli dove la funzione è concava(ovvero volge la concavità verso l’alto)
(imponendo alla derivata seconda d’essere positiva ovvero y’’>0). La risoluzione di tale disequazione restituisce
anche gli intervalli dove la funzione è convessa(ovvero volge la concavità
verso il basso,cioè dove y’’<0);
DOMANDA N.4: Quali sono le principali
differenze tra le Funzioni Algebriche Razionali Intere e le Funzioni Algebriche
Razionali Fratte ?
RISPOSTA:
a) Le Funzioni Algebriche Razionali Intere
sono continue in tutto il loro dominio che risulta tutto R, ovvero "x ' 
mentre le Funzioni
Algebriche Razionali fratte sono discontinue nelle radici (se esistono) del
loro denominatore.
b)
Le Funzioni
Algebriche Razionali Intere non hanno Asintoti; Le Funzioni Algebriche
Razionali Fratte possono avere Asintoti Verticali, Orizzontali oppure Obliqui.
DOMANDA N.5: Dare una Definizione di Funzione.
RISPOSTA: Si definisce Funzione una corrispondenza biunivoca che
associa ad ogni valore della Variabile Indipendente (x) uno e un solo valore
della Variabile Dipendente (y).
DOMANDA N.6: Dare un Concetto di Dominio e di Codominio.
RISPOSTA: Si definisce Dominio l’insieme dei valori che si possono
attribuire alla Variabile Indipendente (x); Si definisce Codominio l’insieme
dei valori associati alla Variabile Dipendente (y).
DOMANDA N.7: Si esponga sinteticamente la Metodologia di Ricerca del
Dominio delle varie funzioni.
RISPOSTA:
a)
Per le funzioni
algebriche razionali intere il dominio è tutto R;
b)
Per le funzioni
algebriche razionali fratte il dominio si trova imponendo al Denominatore
d’essere diverso da zero;
c)
Per le funzioni
algebriche irrazionali intere o fratte con indice dispari il dominio è come le
rispettive funzioni algebriche razionali intere o fratte;
d)
Per le funzioni
algebriche irrazionali intere o fratte con indice pari il dominio si trova
imponendo al Radicando d’essere >=0;
e)
Per le
funzioni trascendenti esponenziali intere o fratte il dominio è come le rispettive funzioni
algebriche razionali intere o fratte;
f)
Per le funzioni
trascendenti logaritmiche intere o fratte il Dominio si trova imponendo
all’argomento d’essere >0.
g)
Per le funzioni
trascendenti goniometriche il dominio, escludendo il suo sottoinsieme che
risulta l’intervallo 0 
x 
2p, è come quello delle rispettive funzioni algebriche
razionali intere o fratte.
DOMANDA N.8: Esporre un concetto di funzione crescente o decrescente in
un intervallo.
RISPOSTA:
a) Una funzione risulta
crescente in un intervallo (a,b) del suo dominio quando, considerati due suoi valori x1 e x2, se
x1<x2 (oppure x1>x2) allora risulterà f(x1)<f(x2) [oppure
f(x1)>f(x2)]. Ciò significa che al crescere(decrescere) della variabile
indipendente (x) devono crescere(decrescere) i valori dei corrispondenti valori
della variabile dipendente (y);
b)
Una funzione
risulta decrescente in un intervallo (a,b) del suo dominio quando, considerati
due suoi valori x1 e x2, se x1<x2 (oppure x1>x2) allora risulterà
f(x1)>f(x2) [oppure f(x1)<f(x2)]. Ciò significa che al
crescere(decrescere) della variabile indipendente (x) devono
decrescere(crescere) i valori dei corrispondenti valori della variabile
dipendente (y).
DOMANDA N.9: Concetto di Asintoto e Ricerca Metodologica dell’Asintoto
Verticale,Orizzontale ed Obliquo.
RISPOSTA: Si definisce Asintoto una retta che tende a toccare la
funzione nei suoi estremi. Esso può essere Verticale,Orizzontale o Obliquo.
·
Per trovare
l’asintoto verticale si svolge il limite per x tendente ad una radice x0
del denominatore della funzione o ad un particolare valore della x e il
risultato è + 
oppure - 
. Il valore x0 è detto punto d’infinito e x=x0
è l’equazione dell’asintoto verticale;
·
Per trovare
l’asintoto orizzontale si svolge il limite per x tendente a - 
o + 
e il risultato deve
essere t (finito). L’asintoto
orizzontale avrà equazione y=t.
·
Nel caso in cui
non esiste l’asintoto orizzontale può essere presente l’asintoto obliquo. La
sua equazione generale è y=mx+q dove m
e q sono due valori che si
devono cercare. Si ha che m è uguale al limite per xà
a - 
o + 
di f(x)/x , mentre q è uguale al limite per xà a - 
o + 
di f(x)-mx .
DOMANDA N.10: Concetto di continuità, di discontinuità e Ricerca
Metodologica dei punti di discontinuità.
RISPOSTA: Una funzione è continua in un valore x0 del suo dominio quando il limite per xàx0 risulta essere f(x0). Si ottiene cioè il punto P=[x0, f(x0)].
Una funzione è continua in un intervallo (a,b) del suo dominio se è continua in
ogni punto di tale intervallo. Se nel punto x0 il limite non è f(x0),
ma è un valore non finito oppure si presenta nella forma 0/0
(Prima forma indeterminata), allora si dirà che in x0 si
presenta un caso di discontinuità. Esistono tre casi di discontinuità dei quali
si presenta ora una relativa Ricerca
Metodologica.
·
DISCONTINUITA’
di Prima Specie: La funzione y=f(x) presenta una discontinuità di prima specie
in x0 se il risultato del
limite sinistro (xàx0-)
risulta essere diverso di quello del limite destro (xàx0+).
La differenza, in valore assoluto, tra questi 2 risultati si chiama SALTO della
discontinuità.
·
DISCONTINUITA’ di Seconda Specie: La funzione y=f(x) presenta
una discontinuità seconda specie in x0 se il risultato del limite per xàx0
risulta - 
o + 
. Il valore x0 è
detto punto d’infinito e x=x0 è l’equazione dell’asintoto verticale;
·
DISCONTINUITA’ di
Terza Specie: La funzione y=f(x)
presenta una discontinuità di terza specie in x0 se il risultato del limite per xàx0 risulta 0/0. La discontinuità è detta
eliminabile. Si svolge poi il limite applicando il Teorema di De L’Hospital.
DOMANDA N.11: Concetto di Simmetria e suoi tipi più importanti.
RISPOSTA: La Simmetria è una
trasformazione geometrica che fa corrispondere alcuni punti ad altri che godono
di particolari proprietà. La Simmetria
può essere CENTRALE o ASSIALE:
- E’ Centrale
quando il centro di essa è un punto P. Se A e B sono due punti simmetrici
rispetto P, allora sarà PA=PB;
- E’ Assiale
quando i punti corrispondenti sono simmetrici rispetto una retta, ovvero
quando è uguale la loro distanza dalla retta.
DOMANDA N.12: Concetto di
Funzione PARI o DISPARI
RISPOSTA:
- Una Funzione
si dice PARI quando è simmetrica rispetto l’asse Y. In pratica ciò avviene quando tutti i
termini della variabile indipendente (x) hanno grado PARI. In questo caso
deve avvenire che f(x)=f(-x);
- Una Funzione
si dice DISPARI quando è
simmetrica rispetto l’Origine degli Assi. In questo caso deve avvenire
che f(x)=-f(-x).
DOMANDA N.13: Illustrare le Ipotesi e le Tesi dei Teoremi di ROLLE e
LAGRANGE e individuare le differenze anche geometriche (con i coefficienti angolari).
RISPOSTA:
·
Ipotesi Rolle:
Data una funzione y=f(x) continua in tutto l’intervallo (a,b), sottoinsieme del
dominio e derivabile nei punti interni di tale intervallo, se f(a)=f(b) ,
allora -àTesi di Rolle: Esisterà
almeno un punto c appartenente ai punti interni di (a.b) per il quale si
ha y’(c)=0;
·
Ipotesi
Lagrange: Data una funzione y=f(x) continua in tutto l’intervallo (a,b),
sottoinsieme del dominio e derivabile nei punti interni di tale intervallo, se
f(a) è diversa da f(b) , allora -àTesi
di Lagrange: Esisterà almeno un punto c appartenente ai punti interni di (a.b)
per il quale si ha y’(c)=
[f(b)-f(a)]/(b-a);
·
La prima
differenza è nelle 2 ipotesi: Per Rolle f(a)=f(b), mentre in Lagrange le 2
ordinate devono essere disuguali; La seconda differenza è che Rolle il punto di
coordinate [c , f(c)] deve risultare un punto di minimo o Massimo, avendo il
coefficiente angolare uguale a zero, mentre in Lagrange in tale punto il coefficiente angolare deve
essere uguale a quello della retta congiungente i punti estremi dell’intervallo
che sono A=[a, f(a)] e B=[b, f(b)].
DOMANDA N. 14: Concetto di
PRIMITIVA di una funzione e suo legame con la derivata
RISPOSTA: Si definisce Primitiva di una funzione y=f(x) un insieme di
funzioni del tipo y=F(x) + c che derivate
restituiscono la funzione y=f(x). Le funzioni primitive si trovano risolvendo
l’Integrale indefinito 
che è quindi uguale a
F(x)+c . Si ha quindi D[F(x) + c] = f(x).
DOMANDA N.15: Dare un
significato pratico dell’Integrale definito di una funzione
RISPOSTA: Quando si svolge l’Integrale definito di una funzione, cioè
per esempio, 
si trova la
superficie della parte di piano
delimitata dalla funzione y=f(x), dalle due rette verticali di equazione
x=a e
x=b e dall’asse delle x.
DOMANDA N.16: Quali sono la
Ipotesi e la Tesi del Teorema di Torricelli?
RISPOSTA: Ipotesi: Data la funzione y=f(x) continua in (a,b) ,
sottoinsieme del suo dominio, per essa si ha à
Tesi: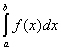 
= F(b) – F(a)
DOMANDA N. 17 : Quali sono la Ipotesi e la Tesi del Teorema di
Torricelli-Barrow ?
RISPOSTA: Ipotesi: Data la funzione y=f(x) continua in (a,b) ,
sottoinsieme del suo dominio, per essa si ha à
Tesi: 
= F(x) + c , dove
F(x) + c sono le primitive della
funzione y=f(x).
DOMANDA N.18: Quando si applica
il Teorema di De L’Hospital e cosa
afferma ?
RISPOSTA: Si applica per risolvere i limiti che si presentano sotto
forma indeterminata 0/0 e/o 
. Afferma che il
limite del rapporto di 2 funzioni che si presenta in una delle 2 forme
indeterminate citate prima è uguale al limite del rapporto delle derivate delle
2 funzioni.
DOMANDA N.19: Come si trovano le ascisse e le ordinate dei punti di
Minimo e Massimo di una funzione y=f(x) ?
RISPOSTA: Per trovare le ascisse si cerca la derivata prima della
funzione e quindi si pone uguale a zero. Per trovare la rispettiva ordinata si
sostituisce l’ascissa trovata alla x nella funzione iniziale.
DOMANDA N.20: Come si trovano
le ascisse e le ordinate dei punti di Flesso di una funzione y=f(x) ?
RISPOSTA: Per trovare le ascisse si cerca la derivata seconda della
funzione e quindi si pone uguale a zero. Per trovare la rispettiva ordinata si
sostituisce l’ascissa trovata alla x nella funzione iniziale.
DOMANDA N.21: Possono gli
asintoti incontrare una funzione e come si trovano gli eventuali punti di
intersezione ?
RISPOSTA:
- L’Asintoto
Verticale non può MAI incontrare una funzione;
- Gli Asintoti
Orizzontale oppure Obliquo (ATTENZIONE: l’uno esclude la presenza
dell’altro) possono incontrare la funzione in qualche punto.
- Per trovare
l’eventuale intersezione si svolge il sistema tra asintoto e curva.
----------------------------------------------
Altre Conoscenze sullo studio delle funzioni si possono trovare
cliccando su à STUDIO FUNZIONI.